传统电网中, 输电网的能量管理(EMS)与配电网的能量管理(DMS)是分开运行的, 并由不同的运行人员独立调控。随着智能电网技术的快速发展, 输、配电网的相互作用也变得越来越显著, 传统输配割裂的能量管理模式也随之受到挑战。例如, 快速发展的分布式发电、负荷响应、电动汽车、分布式储能和配电自动化技术等, 增加了配电网的控制手段, 使得配电网运行方式呈现出更加灵活多变的趋势。这种多变的运行方式也使得配电网对输电网的影响变得更加显著。例如, 在美国加州地区, 2013年底光伏发电量已经达到1200万千瓦。随着光伏的大量接入, 美国加州的净负荷曲线在日出和日落时刻爬坡速率惊人, 3小时内负荷变化可达13000 MW之巨, 对输电网的经济调度造成挑战。而在2011年美国南加州大停电事故中, 事故时配电网恰好处于环网运行, 但是输电网安全分析程序中依然将之当成默认的辐射状运行状态, 从而导致了安全分析中的结果与输电网实际的潮流分布不符, 造成了调度员的错误操作, 使得事故扩大。由此可见, 如果缺乏对输配电网影响的合理评估, 缺乏对输配电网运行的协同管理, 电网运行的经济性、安全性就很难得到保证, 甚至可能出现十分严重的停电事故。
1.为什么要研究输配全局潮流?
众所周知, 一个实际电力系统的输、配电部分在物理上是通过变压器而紧密耦合的, 但为了方便管理, 目前的输、配电网几乎都是由不同的控制中心来进行调控。对于输电网, 通常由EMS软件进行管理, 而对于配电网, 通常由DMS软件进行管理。
潮流计算是EMS和DMS软件中的重要组成, 也是调控电网运行的必要工具。在上述管理模式下, 输、配潮流计算自然也是彼此独立的。具体来说, 计算输电网潮流时, 忽略配电网潮流细节, 仅将后者视为挂靠在输网母线上的负荷注入; 而在计算配电网潮流时, 忽略输电网潮流细节, 仅将后者视为根节点上的理想电压源。如图1所示。
这一输配割裂的潮流计算模式已延续多年。但是, 随着未来智能电网的发展, 配电网分布式电源和自动化装置的增多, 这一模式在潮流仿真时会出现问题, 尤其是在模拟分布式电源出力的间歇性变化, 模拟配电网重构等方面:
大规模分布式电源入网后, 出力的间歇性将会造成输电潮流和配电潮流在边界处的计算结果不匹配, 有明显的电压/功率偏差, 使得系统的真实状态难以通过仿真准确获知;
随着自动化装置增多, 未来配电网重构更加频繁, 甚至出现环网运行的状态, 为获得准确的潮流解, 必须为多馈线配电网指定根节点的合理参考电压, 但在输配割裂的计算模式下, 几乎无法实现这一目的;此外, 配电网中分布式电源的出力变化和有载变压器的档位调节势必对输电网的安全稳定造成影响, 而传统输配割裂的计算模式显然无法考虑这一点。而为了更好地协同输电网和配电网的发电和控制资源, 也需要进行输配全局潮流分析。
因此, 为了提供可靠有效的智能电网分析管理工具, 为输配协同能量管理技术打下牢固基础, 必须研究输配全局潮流。
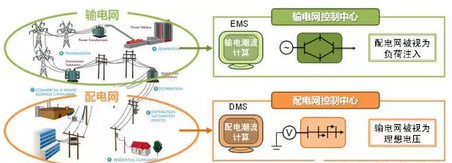
图1 目前的输、配电网的管理模式和潮流计算模式
2输配全局潮流计算难在哪?
直观上看, 输配全局潮流计算并不难, 似乎只要将输、配电网模型拼接在一块直接计算即可。但是这样的集中求解方案在实际上很难行得通。这是因为输配全局潮流计算具有如下的难点:
难点一: 输配全局潮流的模型规模十分庞大;
难点二:输配电网的模型参数相差巨大, 集中求解会出现数值稳定性问题;
难点三: 输配电网的模型分别维护在EMS和DMS软件中, 并且输电网是单相模型, 配电网是三相模型, 模型拼接也比较困难。因此, 基于直接模型拼接的全局潮流集中求解方案并不实用, 必须探求新的解决方案。
3如何计算输配全局潮流?——分布式的主从分裂法
考虑到上述难题, 我们基于主从分裂法, 提出了分布式的输配全局潮流求解方案。这一算法具有如下特点:
针对难点一: 无需进行输配潮流模型拼接, 避免了计算模型规模过大问题;
针对难点二: 分布式计算输、配潮流, 通过迭代交互边界的电压和功率值来消除边界上的计算偏差;
针对难点三: 输、配电网的模型仍然分别在EMS和DMS中进行维护, 通过接口实现边界电压和功率的单-三相转换, 无需交互内部的潮流模型。具体来说, 在这一方法中, 我们首先将输配全局系统抽象为由主系统、边界系统和从系统连接而成的高阶代数系统。其中, 从系统对应输、配电网的边界母线, 主系统为输电网除从系统之外的部分, 从系统则和配电网的边界重合。显然, 主系统和边界系统, 从系统和边界系统之间分别存在耦合, 主、从系统则彼此解耦。
为实现分布式求解, 在算法中引入中间变量代表配电网在边界母线上的总功率注入, 进而将输配全局潮流问题分裂成输电潮流和配电潮流子问题, 进行迭代求解。每次迭代中, 输、配之间交互边界母线的电压和功率值。如果发现某次迭代中边界量的偏差足够小, 算法停止, 得到全局潮流解。算法如图3所示。
图3 主从分裂算法示意图
4主从分裂法有什么特点?
采用主从分裂法计算全局潮流有着一系列的优点。除了上面提到无需模型拼接、模型可以异地维护等优点外, 它还有如下几个优点:
(a) 收敛性有理论保证
在理论上, 可以借助不动点定理证明主从分裂算法具有局部一阶收敛性。在实际计算中, 对于配网辐射状的全局电网, 主从分裂法几乎总是收敛的。如果配电网为强环网, 那么可先将配网的等值支路添加到输电网, 再进行计算, 此时算法也几乎总是收敛的。
(b) 支持分布式计算
显然, 输电网EMS和配电网DMS可以分布式地计算输、配电潮流子问题。分布式架构如图4所示。
(c) 通信量有限
主从分裂算法通常在10次以内便可以收敛, 而每次迭代只需要交互边界上的电压幅值、相角、有功、无功4个变量, 因而总的通信量很小。
(d) 对现有软件的兼容性好
这是因为输、配潮流子问题的形式恰好和现有的潮流计算模型一致, 可以直接调用EMS和DMS中现有的潮流算法求解。
5如何验证方法的有效性?
我们一共构建了5个不同规模的全局电网(从几十节点到几百节点)验证主从分裂算法的效果。在所有的测试中, 主从分裂法计算均准确快速, 迭代次数在7次以内。
为突出进行全局潮流计算的必要性, 我们选出如下两例进行说明。
例1:配电网发生网络重构
考虑配电网从辐射状切换到环状运行。比较全局潮流结果(GPF)和传统模式下的输电网潮流(ITPF)和配电网潮流(IDPF)结果。如表1所示。可见, 配电网络重构对输电网侧的潮流分布造成了影响, 进而又影响到了配电网的潮流分布。由于忽略了输配之间的相互作用, 传统的计算模式造成了高达0.0107 p.u.的电压计算偏差。此时, 必须采用全局潮流计算才能获得准确的潮流结果。
例2: 大规模间隙性分布式能源出力骤降
考虑在输网5节点系统分别接入一个3馈线(F1, F2, F3)的配电网, 其中F3上接有渗透率为50%的分布式能源。由于间隙性, 某一时刻分布式能源处理骤降50%。从图2可以看出, 不仅馈线F3中的节点电压变化, 而且F2中的节点电压也将发生变化。这是由于F2和F3通过输电网耦合在一起。但是统输配割裂的计算结果显然无法反映出这种耦合影响。必须采用全局潮流计算才能获得准确的结果。
6结论和展望
作为未来输配协同能量管理技术的基石, 本文提出了一种基于主从分裂法的分布式输配全局潮流算法。研究表明, 为保证未来智能电网运行的安全性和经济性, 必须进行输配全局潮流计算。所提出的分布式主从分裂算法具有准确、快速的特点, 并且可以充分利用现有的EMS和DMS软件, 符合现有的电网管理架构, 具有良好的工业前景。